组合问题算法题

编程技术 , , , 评论

题目

00112223467899由以上数字组成7个数（如 08 , 12, 29等）要求最大的数字不超过35且至少有2个数不超过15，并且不能重复，请列出所有组合。

算法思想

关于组合问题的求解，可以使用回溯法，path[int]用来存储路径，res[int][int]用于存储结果集，对于去重，可以使用used[bool]来标记该层上一个相同结点的枝是否使用过。本题问题的难点在于如何处理”00112223467899”字符串，是在回溯递归的函数中逐一处理字符串中的字符，还是先将字符串转换为符合条件的int数组，采用后者的方法更为简洁便利。先将”00112223467899”字符串转换为两位数且小于等于35的全排列的int数组vec，然后对vec进行处理。但是还要知道字符串中0~9哪些使用过，所以还需要map<char, int>来标记0~9每个char还剩几个可以使用。

初始化

  1. 初始化map<char, int> map_str，用来表示”00112223467899”字符串中0～9出现的频率;
  2. 将”00112223467899”字符串转换为两位数且小于等于35的全排列数的数组vector<int> vec;
  3. 初始化vec长度的vector<bool> used数组作为backtracking()里的参数，用来判断和标记为同层的树枝是否使用过;
  4. vector<vector<int>> res 该二维数组表示组合结果;
  5. vector<int> path 该数组表示当前的单条路径;

回溯过程

  1. void backtracking(const vector<int> vec, int n, int index, vector<bool>& used)其中const vector<int> vec表示两位数且小于等于35的全排列数的数组，n为元素总个数，index为vec当前的索引号,vector<bool> used用来判断同层相同结点的树枝是否使用过;
  2. 接着就是回溯的过程；可以参考0040.组合总和II;

源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
#include <iostream>
#include <iterator>
#include <algorithm>
#include <vector>
#include <unordered_map>
#include <set>

using namespace std;

namespace std {
	ostream& operator<<(ostream& os, vector<int> vec)
	{
		os << "{";
		for (int i = 0; i < vec.size(); i++) {
			os << vec[i];
			if (i != vec.size() -1)
				os << ", ";
		}
		os << "}";
		return os;
	}
}


vector<vector<int>> res;
vector<int> path;
unordered_map<char, int> map_str;

bool is_valid(int n, int flag)
{
	string str = "";
	if (n < 10)
		str += "0";
	str += to_string(n);
	if (flag == 1) {
		map_str[str[0]]++;
		map_str[str[1]]++;
		return true;
	}
	if ((str[0] != str[1] && map_str[str[0]] >= 1 \
		&& map_str[str[1]] >= 1) \
		|| str[0] == str[1]) {
		if (str[0] == str[1] && map_str[str[0]] < 2)
		     return false;
		map_str[str[0]]--;
		map_str[str[1]]--;
		return true;
	}
	return false;
}

bool is_repeat(vector<int> vec)
{
	set<int> s(vec.begin(),vec.end());
	return s.size() == vec.size() ? false : true;
}

int num_less(vector<int> vec, int n, int min)
{
	int count = 0;
	for (auto x : vec)
		if (x < min)
			count++;
	return count;
}

void backtracking(const vector<int> vec, int n, int index, vector<bool>& used)
{
	if (path.size() == n) {
		if (num_less(path, 2, 15) >= 2 && !is_repeat(path)) 
			res.push_back(path);
		return;
	}

	for (int i = index; i < vec.size(); i++) {
		if (i > 0 && used[i-1] == false && vec[i] == vec[i-1])
			continue;

		if (!is_valid(vec[i], 0))
			continue;
		used[i] = true;
		path.push_back(vec[i]);

		backtracking(vec, n, i + 1, used);

		is_valid(vec[i], 1);
		used[i] = false;
		path.pop_back();
	}
}

vector<vector<int>> combine(string str)
{
	res.clear();
	path.clear();
	map_str.clear();

	string tmp;
	vector<int> vec;
	for (int i = 0; i < str.size(); i++)
		map_str[str[i]]++;
	for (auto x : map_str) {
		tmp = "00";
		for (int t = 0; t < x.second / 2; t++) {
			tmp[0] = x.first;
			tmp[1] = x.first;
			if (stoi(tmp) > 35)
				break;
			vec.push_back(stoi(tmp));
		}
		for (auto y : map_str) {
			if (x.first == y.first)
				continue;
			int t = min(x.second, y.second);
			while (t--) {
				tmp[0] = x.first;
				tmp[1] = y.first;
				if (stoi(tmp) > 35)
					break;
				vec.push_back(stoi(tmp));
			}
		}
	}

	sort(vec.begin(), vec.end());
	vector<bool> used(vec.size(), false);
	backtracking(vec, str.size() / 2, 0, used);
	return res;
}


int main()
{
	vector<vector<int>> myres = combine("00112223467899");
	copy(begin(myres), end(myres), ostream_iterator<vector<int>>{cout,"\n"});
	return 0;
}

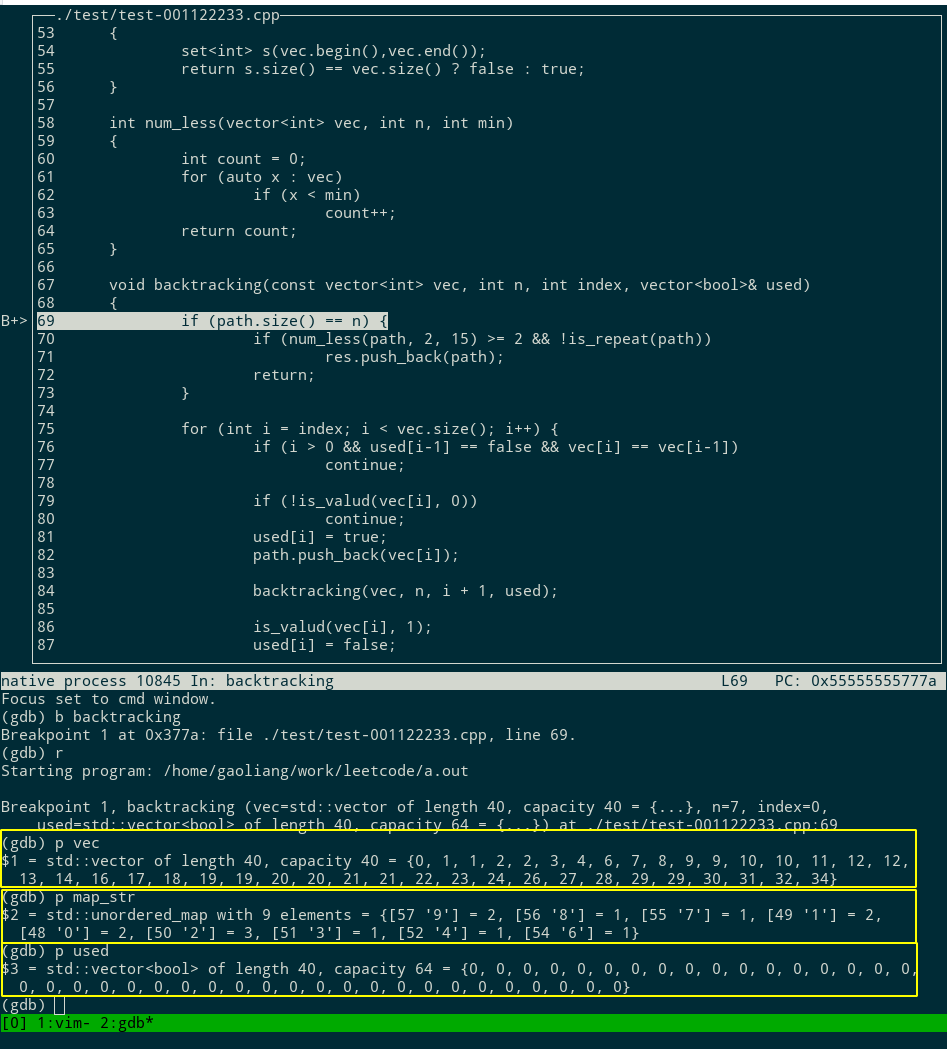
gdb调试过程

初始化后各数组的值

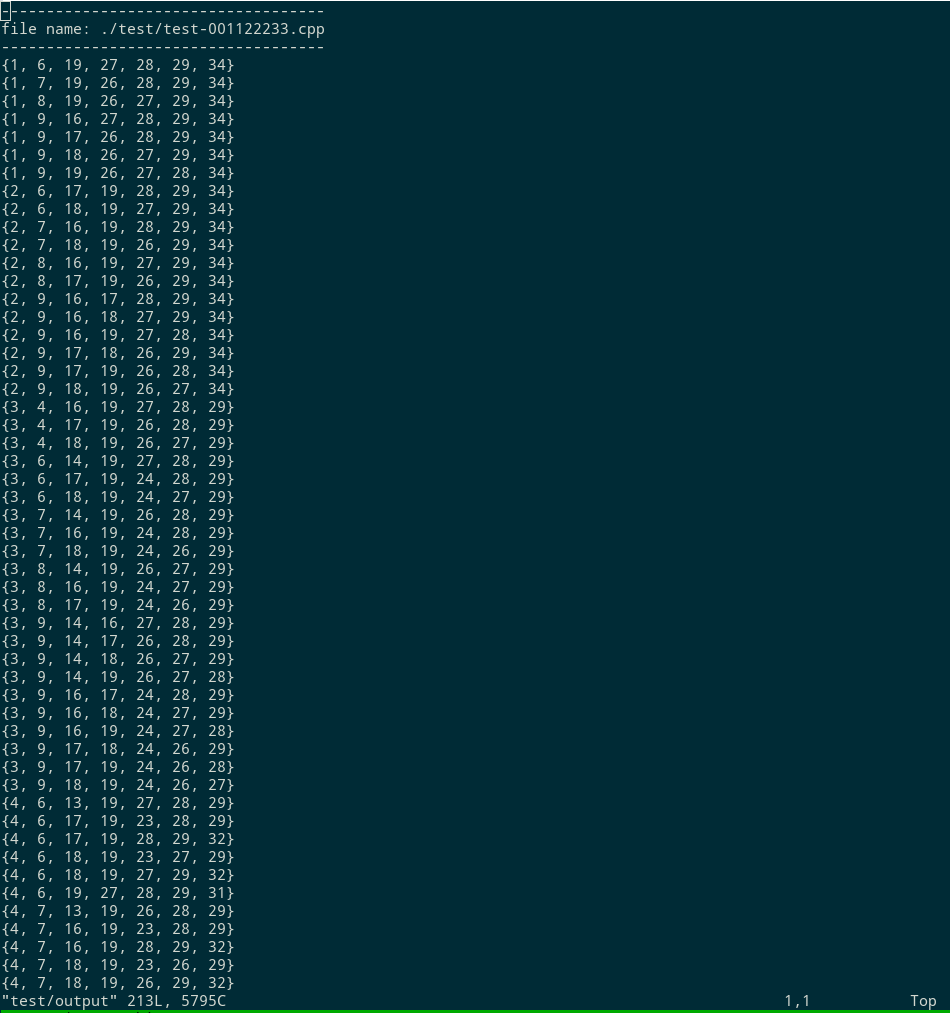
运行结果

AzreallemLinux kernel & C Programmer